

All matter in the universe that has a temperature above absolute zero (the temperature at which all atomic or molecular motion stops) radiates energy across a range of wavelengths in the electromagnetic spectrum. The hotter something is, the shorter its peak wavelength of radiated energy is. The hottest objects in the universe radiate mostly gamma rays and x-rays. Cooler objects emit mostly longer-wavelength radiation, including visible light, thermal infrared, radio, and microwaves.
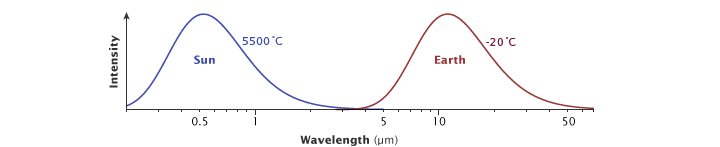
The Sun’s surface temperature is 5,500° C, and its peak radiation is in visible wavelengths of light. Earth’s effective temperature—the temperature it appears when viewed from space—is -20° C, and it radiates energy that peaks in thermal infrared wavelengths. (Illustration adapted from Robert Rohde.)

Incandescent light bulbs radiate 40 to 100 watts. The Sun delivers 1,360 watts per square meter. An astronaut facing the Sun has a surface area of about 0.85 square meters, so he or she receives energy equivalent to 19 60-watt light bulbs. (Photograph ©2005 Paul Watson.)
The surface of the Sun has a temperature of about 5,800 Kelvin (about 5,500 degrees Celsius, or about 10,000 degrees Fahrenheit). At that temperature, most of the energy the Sun radiates is visible and near-infrared light. At Earth’s average distance from the Sun (about 150 million kilometers), the average intensity of solar energy reaching the top of the atmosphere directly facing the Sun is about 1,360 watts per square meter, according to measurements made by the most recent NASA satellite missions. This amount of power is known as the total solar irradiance. (Before scientists discovered that it varies by a small amount during the sunspot cycle, total solar irradiance was sometimes called “the solar constant.”)
A watt is measurement of power, or the amount of energy that something generates or uses over time. How much power is 1,360 watts? An incandescent light bulb uses anywhere from 40 to 100 watts. A microwave uses about 1000 watts. If for just one hour, you could capture and re-use all the solar energy arriving over a single square meter at the top of the atmosphere directly facing the Sun—an area no wider than an adult’s outstretched arm span—you would have enough to run a refrigerator all day.
The total solar irradiance is the maximum possible power that the Sun can deliver to a planet at Earth’s average distance from the Sun; basic geometry limits the actual solar energy intercepted by Earth. Only half the Earth is ever lit by the Sun at one time, which halves the total solar irradiance.
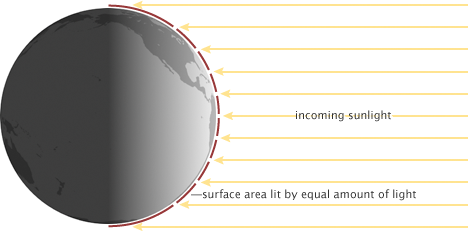
Energy from sunlight is not spread evenly over Earth. One hemisphere is always dark, receiving no solar radiation at all. On the daylight side, only the point directly under the Sun receives full-intensity solar radiation. From the equator to the poles, the Sun’ rays meet Earth at smaller and smaller angles, and the light gets spread over larger and larger surface areas (red lines). (NASA illustration by Robert Simmon.)
In addition, the total solar irradiance is the maximum power the Sun can deliver to a surface that is perpendicular to the path of incoming light. Because the Earth is a sphere, only areas near the equator at midday come close to being perpendicular to the path of incoming light. Everywhere else, the light comes in at an angle. The progressive decrease in the angle of solar illumination with increasing latitude reduces the average solar irradiance by an additional one-half.
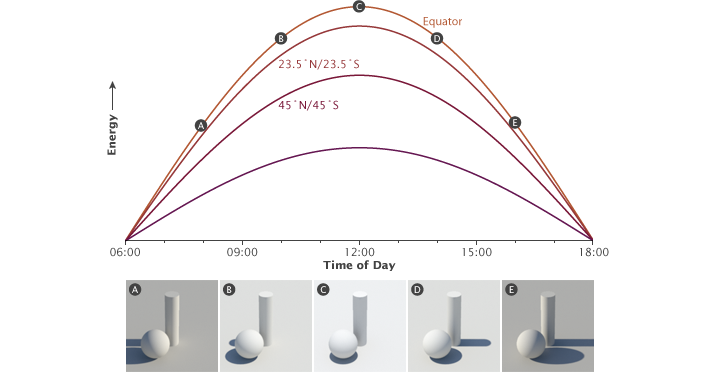
The solar radiation received at Earth’s surface varies by time and latitude. This graph illustrates the relationship between latitude, time, and solar energy during the equinoxes. The illustrations show how the time of day (A-E) affects the angle of incoming sunlight (revealed by the length of the shadow) and the light’s intensity. On the equinoxes, the Sun rises at 6:00 a.m. everywhere. The strength of sunlight increases from sunrise until noon, when the Sun is directly overhead along the equator (casting no shadow). After noon, the strength of sunlight decreases until the Sun sets at 6:00 p.m. The tropics (from 0 to 23.5° latitude) receive about 90% of the energy compared to the equator, the mid-latitudes (45°) roughly 70%, and the Arctic and Antarctic Circles about 40%. (NASA illustration by Robert Simmon.)
Averaged over the entire planet, the amount of sunlight arriving at the top of Earth’s atmosphere is only one-fourth of the total solar irradiance, or approximately 340 watts per square meter.
When the flow of incoming solar energy is balanced by an equal flow of heat to space, Earth is in radiative equilibrium, and global temperature is relatively stable. Anything that increases or decreases the amount of incoming or outgoing energy disturbs Earth’s radiative equilibrium; global temperatures must rise or fall in response.